Optimal associativity in rural areas of Ecuador using game theory

Abstract

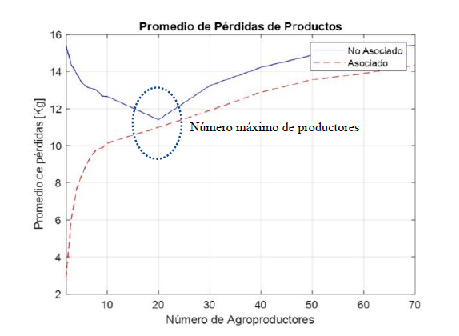
Agriculture in Latin America and specifically in Ecuador seeks to solve self-consumption and sales needs. In Ecuador, thousands of households are currently engaged in agriculture, which represents 70 of the country’s agricultural production and 60% of the food that makes up the basic basket. The objective of this research is to propose a model so that producers can work in agroecological associations using cooperative game theory, achieving to improve their productivity, coming to compete in a dynamism of costs, supply, demand, distance and time. A study with a mixed approach was conducted, since in the quantitative part, semi-structured surveys, descriptive analysis, as well as secondary information for the numerical mathematical model of cooperative game theory were used. In the qualitative part, being a little studied phenomenon, the sample size was 76 agro-producers, and the sampling was for convenience. For its part, the research design was non-experimental, cross-sectional since the data were collected in a single moment (2019). The survey consisted of 13 items, among which were their geographical location, socioeconomic characteristics of the producer and agricultural production, collection-commercialization and sale of the product, among others. The information from the survey was analyzed using descriptive statistics (frequencies, percentages and averages). Finally, using the results of the surveys and secondary databases, their location was georeferenced to simulate two comparative scenarios of working or not in association using the Matlab software. The findings suggest that it is important to work with a maximum of 20 producers per association, with the optimal number being less than 10 agro-producers, thus reducing productivity losses by 6.4% (14.4 kg) of production.